[미적분학] Class2: 삼각 함수와 쌍곡선 함수(그래프와 극한)(2) --- {삼각함수, 쌍곡선함수들의 도함수}

************  이 글은 PC 기준으로 작성되었습니다.   ************

들어가며...

    오늘 공부할 내용은 역삼각함수, 쌍곡선 함수, 역쌍곡선 함수들의 미분형태인 도함수를 공부해보려고 합니다. 오늘은 추가적인 설명이 크게 필요가 없습니다. 단순히 식과 그림을 통해 증명해가면서, 미분 함수는 어떤 형태를 띄고 있는지 보면 될 것 같습니다. 이번 포스팅에서는 글이 그렇게 많지는 않고, 대부분 식이 차지할텐데 순서대로 쭉 따라 나가시면 될 것 같습니다. 추가 설명이 필요한 경우에는 제가 설명을 조금씩 하면서 진행하면, 오늘 클래스는 마무리가 잘 될 수 있을 것 같네요. 그럼 시작하겠습니다!

1. 역삼각함수의 도함수 (Derivative of Inverse Trigonometric Functions)

    1-1. 역사인함수의 미분 (Derivative of Inverse Sine Function)

    그럼, 바로 asin(x)의 도함수를 구해볼까요?

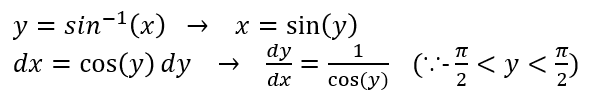
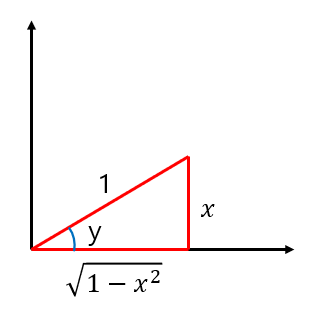
    이때, 도함수는 변수 x에 대해서 표현이 되어야 합니다. 따라서 삼각 함수의 성질을 이용하기 위해 위 사진과 같이 빗변이 1인 삼각형을 그릴 수 있습니다. 그러면, 밑 변과 높이 중 어떠한 변을 x로 두어야 할지가 가장 중요해집니다. 이때 x는 y와 가장 직접인 연관이 있는 변이 되어야 합니다. 다시말해, y는 높이에 의존적이기 때문에, 높이가 x 변수로 잡혀야 합니다. 1-2.를 같이 보시면 좋을 것 같습니다! 그 이후 과정을 더 진행하면,

    따라서, 역사인 함수의 도함수는 이와 같이 구할 수 있습니다. 적분형태는 반대로 진행하면 될 것입니다! 이는 마지막, 정리에서 한번에 다시 정리해 표로 알려드리겠습니다~!

 

 

 

    1-2. 역코사인함수의 미분 (Derivative of Inverse Cosine Function)

    그럼, 바로 역코사인함수의 미분 형태를 알아보도록 합시다!

    사인 함수의 경우, y는 x축과 평행한 밑변의 길이에 의존하기 때문에 밑변을 x로 잡아야 합니다. 그래서 위의 그림과 같은 삼각형을 그릴 수 있습니다. 그리고, 증명을 마저 진행하면,

 

    이렇게, 증명이 가능합니다. 그럼, 다음은 역탄젠트 함수의 미분에 대해 알아볼까요?

 

 

 

    1-3. 역탄젠트함수의 미분 (Derivative of Inverse Tangent Function)

    바로, 역탄젠트함수의 미분을 알아보도록 합시다!

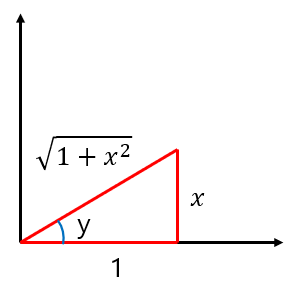
    역탄젠트 함수의 경우, x의 값을 구하는 식을 한번 잘 보시면, 밑변이 1, 높이가 x이어야 한다는 것을 잘 알 수 있을 것입니다. x의 값을 구하는 식은 첫번째 줄의 오른쪽 식을 의미하겠죠? 그럼 이어서 진행해보겠습니다.

 

 

 

 

 

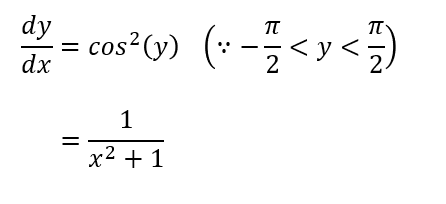
2. 쌍곡선 함수의 미분 (Derivative of Hyperbolic Functions)

    2-1. sinh(x)의 도함수 (Derivative of Sine Hyperbolic Function)

    sinh(x)의 도함수를 구하기 위해서는 대수적인 표현을 이용해야 합니다.

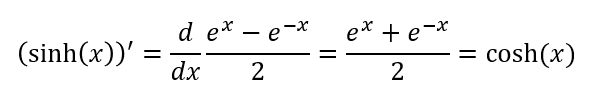
    이렇게 매우 쉽게 증명이 가능합니다. 그렇다면, sinh(x)의 역수 형태인 csch(x)의 도함수도 구해볼까요?

 

    어떤가요? sinh(x) 도함수 구하기 보다는 어렵지만, 그래도 아주 못 할 수준은 아니죠? 이렇게 csch(x)의 도함수까지 구해보았습니다.

 

 

 

    2-2. cosh(x)의 도함수 (Derivative of Cosine Hyperbolic Function)

    cosh(x)의 도함수도 sinh(x)의 도함수를 구할 때처럼 대수적인 표현을 이용합니다.

    역수 형태(sech(x))의 도함수도 구해봅시다!

    별거아니죠? 그럼, 다음은 tanh(x)의 도함수를 알아보러 가봅시다!

 

 

 

    2-3. tanh(x)의 도함수 (Derivative of Tangent Hyperbolic Function)

    그럼, 바로 tanh(x)의 도함수를 구해봅시다!

    2-1, 2-2보다는 어려워졌어도 그래도 할 만하죠? 이번엔 coth(x)의 도함수를 구해보도록 합시다.

    어땠나요? 그렇게 어렵지 않게 따라올 수 있었죠? 그렇게 어렵지 않은 미분과 증명이니 꼭 스스로 해보도록 합시다!

 

 

 

 

 

3. 역쌍곡선함수의 미분 (Derivative of Inverse Hyperbolic Functions)

    3-1. asinh(x)의 도함수 (Derivative of Inverse Sine Hyperbolic Function)

    역쌍곡선 함수를 미분하는 경우, 우리가 이전 클래스에서 구했던 대수적 표현의 함수를 직접 미분해도 되지만 더욱 쉬운 방법을 통해 미분함수를 구해보도록 하겠습니다. 그리고, 대수적 표현의 함수를 미분하는 방식은 직접 도전해 보도록 합시다. 그럼, 도함수를 구하는 과정을 살펴볼까요?

 

    식만 복잡해보이지, 그렇게 어렵지는 않았죠? 다음은 acosh(x)의 미분입니다. 3-2로 넘어갑시다!

 

 

 

    3-2. acosh(x)의 도함수 (Derivative of Inverse Cosine Hyperbolic Function)

    acosh(x)의 도함수를 그러면, 한 번 바로 구해보도록 합시다!

    어떤가요? 구하는 방식이 asinh(x)를 구할 때와 매우 비슷하죠? 이렇게 구했다고, 끝나는 것이 아니라, 한 번, x와 y의 범위가 저렇게 되는지 생각해보세요! 범위를 생각하는 것이 이 미분에 있어서 가장 중요한 포인트랍니다! 다음은 atanh(x)의 미분입니다. 3-3으로 넘어갑시다!

 

 

 

    3-3. atanh(x)의 도함수 (Derivative of Inverse Tangent Hyperbolic Function)

    바로 atanh(x)의 도함수를 구해보도록 해요!

    어땠나요? 그래도 앞선 3-1, 3-2보단 어려운 감이 없지않아 있죠? 세번째 줄이 잘 넘어가지 않는다면, Class1에서 공부한 쌍곡선 함수의 성질을 다시 한 번 복습하고 오면 좋겠습니다. 오늘 공부한 내용은 여기까지이며, 4.에서 다시 한 번 복습하고 마무리짓도록 하겠습니다!

 

 

 

 

 

4. 마무리... 도함수들의 정리

삼각함수 도함수는 쌍곡선함수 도함수와 역삼각함수 도함수는 역쌍곡선함수 도함수와

서로 서로 비교해가면서 확인해보세요!

 

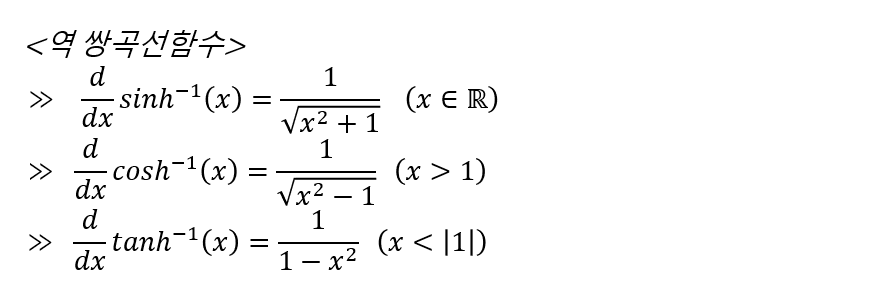
오늘의 클래스는 여기까지입니다. 다음 클래스에서는 로피탈 정리를 이용한 극한, 점근선, 극한의 엄밀한 정의 등을 공부해보도록 하겠습니다! 질문은 댓글로 언제나 받습니다! 감사합니다! 오늘도 좋은 하루 보내시길 바랄게요~! 다음 클래스 포스팅으로 뵙겠습니다! 그때까지 안녕히 계세요~!!