[미적분학] Class4: 미분의 응용(1) --- {일차 근사와 전미분}

************  이 글은 PC 기준으로 작성되었습니다.   ************

들어가며...

    오늘 공부할 내용은 일차 근사(Linear Approximation)과 전미분(Total Differential)입니다. 이번 클래스는 증명에 기반을 두고 있습니다. 그리고 그 증명을 통해 근사를 해보려고 합니다. 우리가 이 미분을 활용 및 응용을 하는 이유는 결국 근사를 위해서 존재합니다. 일차 근사는 무엇이고, 전미분은 또 무엇이며, 서로 어떻게 다른지(전미분 문단에서) 다뤄 보도록 하겠습니다. 이번 포스팅에서는 글을 잘 읽으면서 따라오시면, 크게 어렵지 않으실 것입니다! 그렇게 하면, 오늘 클래스는 마무리가 잘 될 수 있을 것 같네요. 그럼 시작하겠습니다!

1. 일차 근사 (Linear Approximation)

    미분의 기본적인 아이디어로부터 근사법을 알아낼 수 있습니다. 미분의 의미는 한 특정 Point(점)에서의 순간 변화율(순간적인 기울기)입니다. 그래서, 특정 point 기준으로 충분히 작은 범위 내에서, 이 정도 증가 혹은 감소 했겠구나 추정하는 방식입니다. 충분히 작은 범위이어야 하는 이유는 범위가 커질수록 근사값과 실제값이 벌어질수도 있기 때문입니다(당연한 이치죠. 이해가 안 되신 다면, 아래의 사진을 참고해주세요). 아주 우연하게 실값과 일치할수도 있지만, 아주 작은 확률이며 거의 모든 상황에서 무시하지 못할 만큼의 오차가 발생합니다.

    실제적으로 식을 통해 일차 근사를 어떻게 하는지에 대해 알아보기 전에 일차 근사가 무엇인지부터 그 의미를 다시 짚어 보겠습니다. 일차 근사. Linear Approximation. Linear: Line의 형용사형. 한글로 보면, 무슨 의미인지 정확하지 않지만, 영어는 꽤나 명확합니다. Line, 즉 직선에 대한 근사라는 것입니다. 다시말해, 한글 명칭의 '일차'는 '일차 함수'를 의미하게 됩니다. 그렇다면, 일차 근사는 이렇게 정리해볼 수 있습니다. 어떤 함수의 어떤 특정한 점에서 미분과 일차함수를 이용한 근사법. 어떤가요? 어느 정도 감이 오시나요? 일차 근사는 무엇과 유사하다고 생각이 드나요? 맞습니다! 바로 접선의 방정식입니다!! 이렇게 말씀드린다면, 한 번에 이해가 가시죠?

    결국에는 이 일차 근사가 의미하는 바는 접선의 방정식입니다. 접선의 방정식은 고등학교 때 모두 배웠다고 생각하며(그리고 이전 클래스에서 접선의 방정식을 응용하기도 했기에), 바로 식으로 넘어가 보겠습니다.

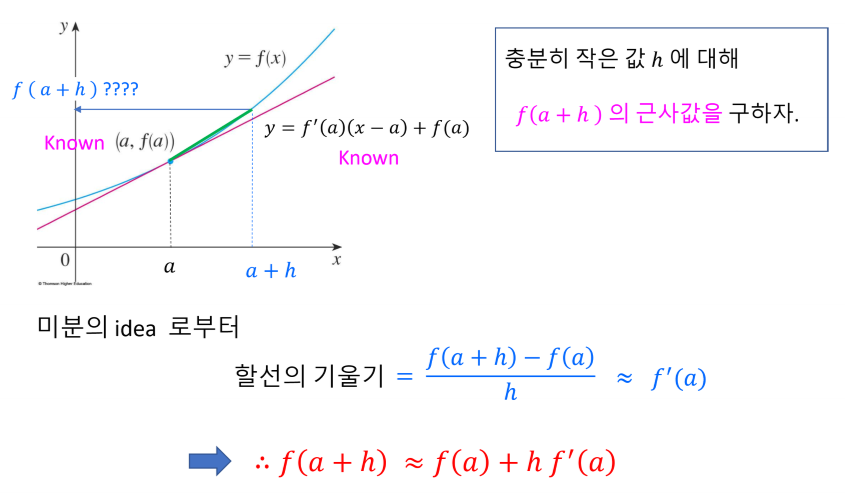
출처: 안소영 교수 PPT 자료      제가 그리기가 조금 귀찮아서... 인터넷에서 가져왔습니다... ㅎㅎ

출처: 안소영 교수 PPT 자료      제가 그리기가 조금 귀찮아서... 인터넷에서 가져왔습니다... ㅎㅎ

 

    그렇다면, 이번에는 직접 응용을 해보도록 합시다.

    실제 계산기를 이용해 구한 값은 1.99499373... 입니다. 이렇게 봤을 때 이러한 근사법이 꽤나 정확하다는 것을 알 수 있겠죠? 사실 근사법은 이것만 있는 것은 아닙니다. 이후에 이러한 다항함수 근사를 1차, 2차, 3차, ..., n차까지 늘리면, 그것이 바로 테일러 근사(Taylor Approximation)이 됩니다. 이 근사법은 나중에 다루도록 하겠습니다. 그렇다면, 이제 다음 주제로 넘어가 봅시다.

 

 

2. 전미분 (Total Differential)

   전미분은 미분법을 활용하여 만든 굉장히 편리한 미분법입니다. 미분법을 활용해 또다른 미분법을 만들어내다니.. 참 황당하죠? 하지만, 전미분은 미분법으로 사용할 수도 있지만, 근사법으로도 활용이 가능합니다. 그리고, 그 형식이 위에서 배운 일차 근사와 꽤나 비슷합니다. 이 전미분의 경우, 텍스트로 읽기보단, 일단 한 번 부딪혀봐야 감이 옵니다. 그럼, 그래프와 함께 보면서, 전미분을 유도해보도록 합시다!

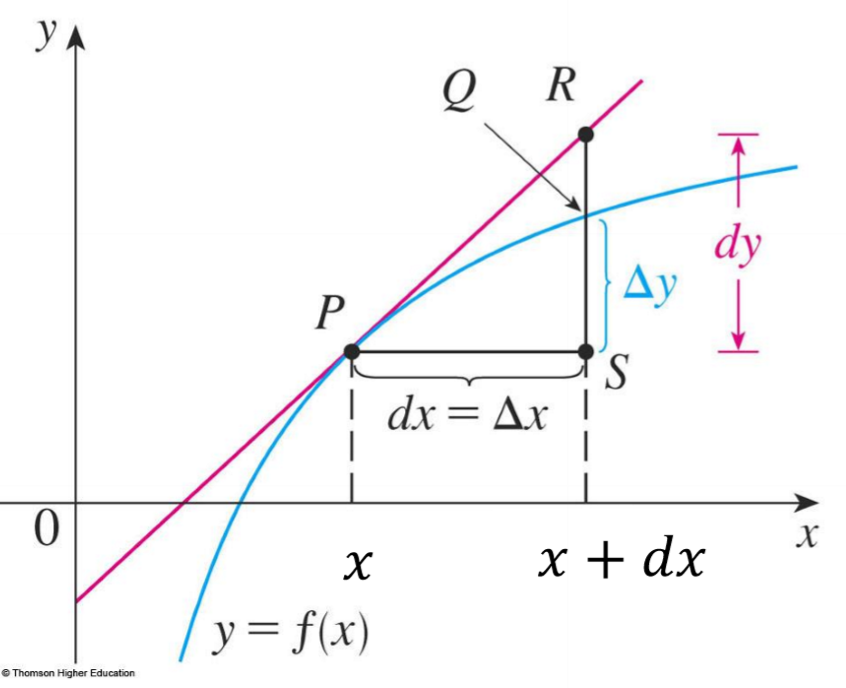
   점 P에서의 접선은 일차 근사된 직선입니다. 그리고, 충분히 작은 Δx와 dx에 대해서, x+Δx에 대응하는 실제 그래프에서의 실값과 P점의 y좌표 차를 Δy라 하고, 일차 근사된 직선에서의 값과 P점의 y좌표 차를 dy라 합니다. 그러면, 다음과 같은 과정을 통해 전미분을 증명할 수 있습니다.

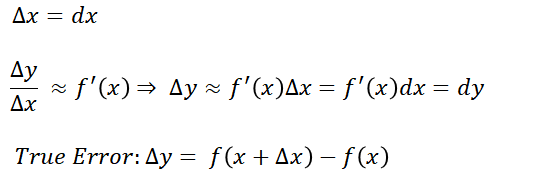
   식은 참 간단한데... 그럼 이 식이 의미하는 게 뭘까요? 결국엔 Δx, Δy를 충분히 작은 범위 내에서 각각 dx, dy로 근사하여 계산이 가능하다는 것입니다. 그렇다면, 이 미분법은 어떻게 사용할까요? 아래와 같은 식이 주어졌고, 이 식의 dy/dx를 구해야 한다고 하겠습니다.

   위의 증명을 변형(여기서는 다루지 않습니다)해 다시 새로운 형태의 전미분이라는 미분법을 만들어내게 됩니다. 바로, 각 항에 대하여 하나의 변수에 대해서만 미분을 하고, 그 항 뒤에는 미분한 변수의 증분을 써줍니다. 대신, 이때 각 항은 함수에 대해서 곱의 미분법을 따릅니다. 이러한 미분후에, dy/dx로 정리해주면, 답을 얻을 수 있습니다. 참... 말이 어렵죠? 식을 직접 보면, 이해가 가실겁니다.

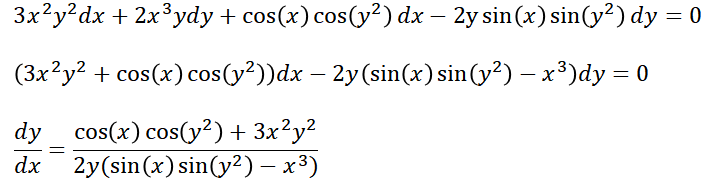
   쉽게 말하면, f(x)g(y)h(z) 이렇게 3변수 함수가 있다고 하더라도, x에 대해서 미분을 하려고 한다면, x에 관련없는 g(y)h(z)는 x에 대해 상수 취급이 됩니다. 대신, f(x)g(y)h(z) 자체는 곱의 미분법을 따르니, f미분, g미분, h 미분을 각각 해주어야 겠죠. 그렇게 되면, f'(x)g(y)h(z)dx + f(x)g'(y)h(z)dy + f(x)g(y)h'(z)dz를 만족하게 됩니다. 위의 문제는 이 경우가 아닌 2변수 함수에 대해서로 줄이면, 딱 맞아 떨어지죠.

 

   그럼, 이번에는 이 전미분을 근사법에 어떻게 사용하는지 알아보도록 하겠습니다! 한번, 2 - √(4.05)의 일차 근사값을 구해야 한다고 해보겠습니다. 이때, 가장 중요한 부분은, 근사값을 구하기 위해 가장 적절하면서도 가장 간단한 함수를 가정하는 것입니다. 이러한 경우, 일반적으로 f(x) = √(x)로 잡을 수 있습니다. 이후의 단계는 아래를 봅시다.

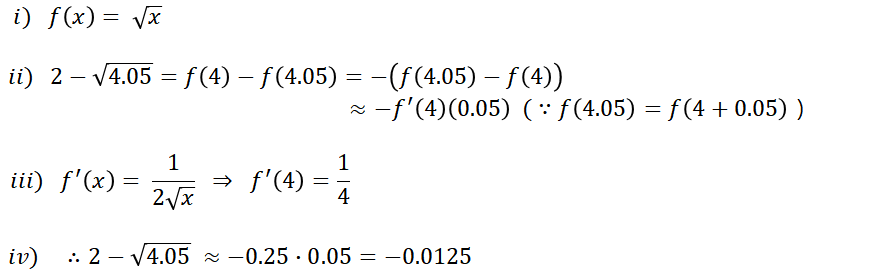
   ii)에서 잘 보시면, f(4) - f(4.05)는 True Error에 해당합니다. 그리고 True Error인 Δy를 이용하여 f'(x)Δx로 간다면, 아주 쉽게 이해하시고 푸실 수 있으실겁니다. 이렇게 전미분을 통해 근사값을 구하는 방법을 공부해보았습니다. 

 

 

 

 

 

오늘의 클래스는 여기까지입니다. 다음 클래스에서는 이제 기본 적분을 공부해보도록 하겠습니다! 질문은 댓글로 언제나 받습니다! 감사합니다! 오늘도 좋은 하루 보내시길 바랄게요~! 다음 클래스 포스팅으로 뵙겠습니다! 그때까지 안녕히 계세요~!!